Modeling the European Neolithic expansion suggests predominant within-group mating and limited cultural transmission

One-dimensional equation model

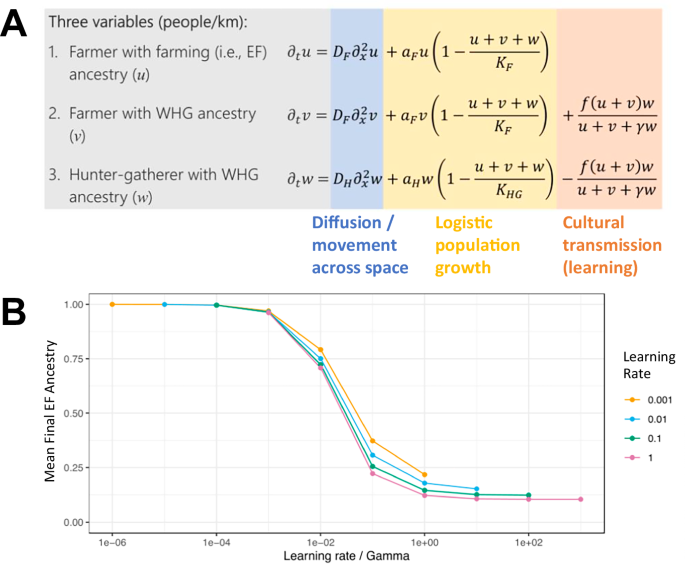
We set up a reaction-diffusion model, based on partial differential equations, which incorporates spatial diffusion of individuals, cultural transmission of farming practices, and genetic ancestry at a single locus. Under this model, we assumed a 3000 km long one-dimensional (1D) habitat along which the density of three types of individuals is modeled: cultural farmers with EF ancestry, cultural farmers with WHG ancestry, and cultural hunter-gatherers (HGs) with WHG ancestry. As an initial condition, we assume that the farmers with EF ancestry are constrained to ~ 200 km at one end of the range, and the HG group is constrained to the remaining 2800 km of the range, with about a twenty-fold difference in population density²⁹. Our mathematical model assumes a diffusion component, a logistic population growth component, and a cultural transmission component (see formulas in Fig. 1A; for a comprehensive description of the symbols and components of the equations in Fig. 1A, see Supplementary Note 1). The cultural transmission model was originally developed by Fort (2012)³¹, and accounting for haplogroup frequency at a single genetic marker by Isern et al.⁵¹. The cultural transmission component of our model decreases the HG density and to the same extent increases the “farmers with WHG ancestry” density as a function of two parameters, the learning rate f and the bias parameter γ. The learning rate f is a product of the number of teachers an HG contacts during their lifetime, and the probability that an HG converts to farming after contact with a farmer. The bias parameter γ modifies the preference of HGs to learn from a farmer rather than from another HG³¹. The diffusion constant D was chosen such that the expansion speed of farming under purely demic parameters is the empirically observed 1 km per year, given a growth rate ɑ of 3% per year^29,85. We assumed that both farmers and HGs have the same diffusion constant and growth rate. In accordance with the initial condition, we assumed that the carrying capacity of farmers was twenty times larger than that of HGs²⁹. We set up the partial differential equations model in Mathematica 13.3⁸⁶ and numerically solved it over a time span of 100 generations (i.e., ~ 2500 years when assuming a generation time of 25 years), which was shortly after all HGs had been acculturated, using the Mathematica function NDSolve. The boundary conditions of the numerical solution were set up such that at positions 0 km and 3000 km (the left and right boundary of the 1D landscape), the first derivative of the three population densities with respect to the space coordinate was set to zero across all time points.

Two-dimensional agent-based simulation model

Using the insights from the basic 1D reaction-diffusion model, we then developed a more realistic two-dimensional (2D) agent-based model, written in the Eidos language⁸⁷ designed for the SLiM simulation framework⁵⁷ (v4.0). In these simulations, each individual exists on a simulated 2D landscape, has a diploid genome, and a cultural identity (farmer or HG). We adopt annual timesteps and model overlapping generations, meaning that individuals persist across multiple yearly intervals until they pass away. Upon initialization of the simulation (year one), the ancestry assigned to the individuals’ chromosomes is based on their initial cultural identity (i.e., farmers have pure EF ancestry and HGs have pure WHG ancestry). In each subsequent year, the ancestry proportion of new offspring is determined via sexual recombination of the individual’s parental genomes. The cultural identity of each individual is independent of their genetic ancestry and can change from HG to farmer through means of cultural exchange as the simulation progresses.

Genome simulation

To determine the ancestry proportion of each simulated individual, one neutral marker mutation is initialized every megabase along the 247 Mb simulated chromosome (human chromosome 1) of all farmers. Therefore, since we consider diploid individuals, each individual has a simulated genome of 247 * 2 = 494 markers. All initial farmers have all 494 markers, which are set to equal “1”. These markers “tag” EF ancestry along the chromosome of each individual. All initial hunter-gatherers have all markers equal to “0”. Accordingly, the proportion of EF ancestry is calculated in all individuals subsequent to year zero by counting the number of markers equal to one and dividing by the total number of marker locations (i.e., by 494). The genomes of new individuals are generated via simulated sexual recombination of the two parents as part of the built-in SLiM reproduction function⁵⁷, assuming a recombination rate of 1 cM/Mb. This function takes the two parental genomes and simulates crossing over between the two gametes at the specified recombination rate⁵⁷ and is explained in more detail in Supplementary Note 4.

Mortality and competition

Mortality in our agent-based model is governed by two main factors: age-dependent mortality and density-dependent competition. Our age-dependent mortality curve is based on osteological age-at-death data^42,55. We generated an age-specific ‘equilibrium’ mortality rate that is applied to both farmers and hunter-gatherers, which corresponds to the age-at-death distribution observed in the osteological data^42,55 (Supplementary Data File 3, 4; Supplementary Note 5; Supplementary Fig. 7), i.e., in equilibrium, this mortality rate leads to the age-at-death distribution observed in the osteological data^42,55. Using these ‘equilibrium’ mortality rates for each age, we computed an equilibrium fertility rate of 0.1 for each mature individual over the age of 11. I.e., this fertility rate compensates for yearly deaths, which allows the population size to stay constant over time in regions where it has reached the carrying capacity. The ages of individuals at the initiation of the simulation were sampled from the equilibrium age distribution. Our primary age-specific mortality rates (Supplementary Data File 3; Supplementary Fig. 7) correspond to the age-at-death distribution observed by Papathanasiou⁴², but to assess if different mortality curves impact our results, we sought out an alternative mortality curve based on Eshed et al.⁵⁵ (Supplementary Fig. 7; Supplementary Data File 4). We ran simulations with this alternative curve to evaluate the robustness of our inference to the assumed mortality rates.

To model density-dependent competition—based on the idea that increased density leads to higher health-related mortality costs^14,88,89—we implemented a density-dependent scaling of the ‘equilibrium’ mortality curve. In our agent-based model, density-dependent competition is determined by the total local population density, regardless of cultural identity, and this is compared to the carrying capacity specific to each group. This approach is consistent with our reaction diffusion model, in which both farmers and hunter-gatherers contribute equally to population pressure. To this end, all age-dependent mortality rates were scaled down in regions with population density below K, and scaled up in regions with population density above K. The local population pressure is calculated as the ratio of the number of neighbors within a radius of 30 km surrounding each individual, relative to the expected local K (or the expected number of individuals in this area calculated using the carrying capacity). We derive each individual’s ‘experienced’ mortality rate by multiplying its ‘equilibrium’ mortality rate by the local population pressure, which allows the population to grow until it hits the carrying capacity K. Each cultural group has a unique carrying capacity— K_F for farmers, and K_HG for HGs, which allows farming to support higher population densities.

We set the K_HG to 0.064 individuals per square kilometer. This is following the modeling approach by Currat and Excoffier⁵⁴, who selected this value based on two previous papers exploring palaeo-demographics^90,91. For the farmer carrying capacity (K_F), we used a value of 1.28 individuals per square km. We calculated this number based on estimates by a model by Ammerman and Cavalli-Sforza (1984). In this model, the K_F is expected to be 20 times larger than K_HG²⁹.

We assume a constant fertility rate of 0.1 per mature individual per year (see Reproduction and within-group mating section below). The age-specific mortality curve is scaled by population density such that, at carrying capacity, the number of deaths balances the number of births, maintaining a stable population size. At lower densities, mortality decreases, allowing the population to grow toward the carrying capacity. In our model, density-dependent competition takes into account all individuals, independent of cultural identity. As a result, HG populations gradually decline over time as the population pressure from close by farming populations becomes too large for their smaller K_HG. This is based on the idea that farmers compete with HGs for land and resources, which was also incorporated in previous mathematical models of the farming expansion^36,37,38. To reduce the significant runtime and memory requirements of the agent-based simulation, we downscaled the number of individuals by a factor of five. Thus, we divided all carrying capacities mentioned above, as well as the starting population density, by 5 for all agent-based simulation runs. This results in an average runtime of 4-5 days on a computing cluster using 20 Gb or less of RAM per individual simulation.

Reproduction and within-group mating

Each year, each mature individual randomly chooses a mate within its cultural group (within-group mating) or independent of cultural group (between-group mating), governed by a within-group mating probability parameter set before runtime. In addition, mate selection only occurs between mature individuals (age > 11) within a radius of 10 km. When a suitable mate is found, then the number of offspring is sampled from a Poisson distribution with rate parameter λ = 0.1 using SLiM’s⁵⁷ built-in pseudorandom number generator. This produces a non-negative integer number of offspring per mating event, drawn according to the Poisson probability mass function. This rate is calculated based on the age-specific mortality curve, such that population size is maintained when the population is at carrying capacity (i.e., deaths are compensated by births; see above). If no suitable mate is found (e.g., if an HG is set to mate within-group, but is not surrounded by any other HG within a radius of 10 km), then no offspring is produced by that individual in that year, except if it is selected as a mate by another individual. The location of offspring is chosen as one of the parents’ locations, simulating maternal care.

If a HG and a farmer reproduce, their offspring is assigned to be a farmer. This assumption is supported by cultural observations of the assimilation of individuals into farming groups^73,74, and the lack of farming ancestry in the genomes of HGs in ancient DNA studies^75,76. However, we have validated the robustness to this assumption with a model where offspring of farmer-HG matings randomly choose their subsistence strategy (Supplementary Fig. 13).

Learning and cultural transmission

Each year, every HG individual has the opportunity to learn agriculture and transition to being a farmer. The individual probability of transitioning to farming takes into account the local proportion of farmers surrounding the HG individual in a radius of 10 km (i.e., the more farmers there are in the vicinity, the higher the probability of learning; when no farmers are nearby, learning will not take place). Thus, for each HG in the simulation at a given year, the transitioning to farming is a random event with probability calculated as the product of the local proportion of farmers and a simulation-wide learning rate f (assuming γ = 1, as justified in the first section of Results). This model is consistent with the cultural transmission model of Fort (2012)³¹. The product of the fixed number of teachers encountered each year and the probability of learning farming from a single farmer contact, in their model, equals our learning rate f. It can be interpreted as the ‘number of HGs converted per farmer’ when the local proportion of farmers is close to zero (i.e., at the tip of the wave-front of the farming expansion), or alternatively as the proportion of HGs that gets converted to farming when farming is the dominant local subsistence strategy. Further note that our rates are yearly rates, whereas Fort (2012) models cultural transmission on a per-generation basis³¹.

Simulation landscape

The landscape map in our model is represented by a black-and-white image file that is utilized by SLiM⁵⁷. The black pixels represent inhabitable land, and the white represents uninhabitable regions (i.e., oceans). Within our 2D spatial model, each individual has a positive X and Y coordinate that represents their location on the inhabitable landscape. The 2D position of the individuals is compared to the location on the landscape map, allowing us to achieve geographic boundaries for expansion.

We used this feature to run simulations on both a simple all-black pixel plane where all regions of a 3700 × 3700 km landscape are inhabitable, as well as a map outlining the geography of Europe. The latter map was adapted from the European Environmental Agency’s (EEA) Elevation map of Europe⁵⁸, available at the following URL: (https://www.eea.europa.eu/ds_resolveuid/558D91E1-3DB0-4639-9F70-2012CC4453A5). Using Adobe Photoshop (CC 2022)⁹², we made the landscape image file dichromatic by selecting the land areas and filling them with black pixels, whereas we changed the remaining pixels (i.e., oceans) to white. To facilitate water travel via ocean, we added water crossings to the map using the directional maps from Fort (2015) as reference³² (Supplementary Fig 6). The same process was used for the simulations that modeled multiple distinct routes. However, in these versions of the landscape map, additional maps were overlaid on top of the base map that corresponded to the coastal route and the Danube/Rhine routes. These overlays (Supplementary Figs. 8 and 9) allowed us to check if individuals were located on a route that facilitated a greater dispersal potential (see below for more detail on the movement of individuals).

Movement

Each year, for every individual, a distance in the X-direction (East-West) and a distance in the Y-direction (North-South) is drawn from normal distributions with standard deviations σ_X and σ_Y, which are then added to the individual’s previous X, Y position. These standard deviations allow us to control the distance individuals can travel within a year. Whenever the coordinates of the newly sampled position are out of bounds (i.e., off the map or on a white pixel of the landscape), this position is rejected, and a new position is sampled until a legitimate position is found.

For most simulations, we assume isotropy, i.e., σ_X and σ_Y are the same. However, we explore a model with σ_X > σ_Y to investigate the impact of a favored East-West movement direction, e.g., reflecting the faster expansion along the Mediterranean route^45,56,69. In addition, we explored another model of biased dispersal, where we added a coastal route to the landscape (Supplementary Fig. 8). In this model, when individuals were located along ocean waterways or along the Mediterranean coast, they had a slightly increased dispersal distance based on coastal expansion speed calculations from Fort & Pérez-Losada⁵⁶. Individuals only had this increased dispersal associated with the route if they continued traveling along the route. The likelihood of them continuing along the route or leaving was randomly sampled at equal probability. If an individual left and returned to the greater continental area, they would revert to the standard continental σ_X and σ_Y. In these more complex landscape simulations, we also incorporated mountainous regions as barriers to dispersal⁴⁵ (Supplementary Fig. 8). White pixels were added to the map based on regional topography⁵⁸. The combination of the physical barriers and the waterways enforced distinct routes of expansion across the landscape.

Finally, we developed another biased dispersal model, again with mountainous barriers⁵⁸ as well as larger dispersal distances along both the Mediterranean Coast and the Danube-Rhine Corridor, relative to a smaller dispersal distance in the greater continental area (Supplementary Fig. 9). For these simulations, we kept both σ_X and σ_Y the same (3 km), but we increased σ_X and σ_Y for individuals along the Mediterranean Coast (30 km) and the Danube-Rhine Corridor (15 km). These values are based on work by Davison et al., (2006), who found 10x faster dispersal along the Mediterranean Coast and 5x faster dispersal along the Danube-Rhine Corridor⁴⁵. To accommodate for the increased dispersal along the waterways while still maintaining an overall front speed of ~ 1 km per year, we needed to reduce the base σ_X and σ_Y from the 5 km we used in other models to 3 km.

Front speed calculation

Our simple square landscape was used to investigate how front speed, i.e., the speed with which farming expands across the X-axis of the square, depends on step size and learning rate parameters. Upon initialization, we filled up the landscape with individuals in accordance with the HG carrying capacity (K_HG). Individuals with X-coordinates between 0 and 74 km were designated as original farmers, while the rest of the individuals on the map were initialized as HGs. We then tracked the expansion of farming each year by calculating the proportion of farmers within twenty 185 km wide bins on the X-axis. The extent of farming expansion was defined as the X coordinate of the bin at which the farmer proportion had just reached 50%. The speed of farming expansion was then calculated by the slope of a linear regression of the extent of farming against time.

Empirical ancestry estimates

We used qpAdm⁶² from the ADMIXTOOLS2⁹³ package with parameters ‘allsnps = TRUE’ and ‘afprod = TRUE’ to obtain empirical estimations of EF, Steppe, and WHG ancestry contributions to Neolithic aDNA samples from Europe (Allen Ancient DNA Resource (AADR) v62.0)⁶¹. Including Steppe as a source population allowed us to filter individuals from our dataset that contained Steppe ancestry or possible modern contamination. i.e., by filtering out these individuals, we were able to capture the population dynamics unique to the farming expansion. Following Patterson et al.⁶³, we formed the WHG source population by grouping 18 ancient hunter-gatherer individuals^{53,64,65,66,68,79,94,95,96}, 19 individuals for the Steppe population^{7,53,62,63,97,98}, and formed the EF population from 21 individuals from the Balkans and Aegean^7,53,62,99. We supplied the following four groups as fixed right-group populations in qpAdm⁶²: Russia_Afanasievo⁹⁷, WHGB^53,100,101, Turkey_N^7,102, and OldAfrica^103,104. We restricted our analysis to individuals dating between 5000 and 8500 ybp and filtered any related individuals or those assigned as contaminated in the AADR metadata, resulting in 1675 individuals. We classified qpAdm⁶² models as plausible with p-value ≥ 0.01 and admixture weights between 0-1. To increase the confidence in our EF and WHG ancestry estimates, we restricted our qpAdm⁶² analysis to individuals with admixture weight standard errors 63, and individuals with less than 5% Steppe ancestry, resulting in a final set of 618 individuals. Ancestry estimates of the 618 ancient individuals, plotted geographically through time, can be found in Supplementary Fig. 16). In our qpAdm⁶² analyses, we used Balkan_N as the proxy source population for Early Farmer (EF) ancestry, reflecting previous recommendations⁶³. While not the earliest point of Neolithic expansion, Balkan_N serves as a geographically and genetically intermediate farming population that provides broad utility as a proxy source across European Neolithic contexts. Notably, Balkan_N individuals were selected to possess minimal hunter-gatherer admixture⁶³, which improves qpAdm⁶² model fit typically yielding higher p-values when modeling admixed Neolithic populations in Europe. To further stabilize ancestry estimates, we included Turkey_N and a set of deep outgroups in the right populations (see full list in Supplementary Data File 1). As a consequence of using Balkan_N, which has minimal WHG ancestry, some ancient samples—especially those from southeastern Europe or regions east of the Balkans—can yield slightly negative WHG ancestry estimates, while samples from northern and northeastern Europe (particularly those younger than 7000 ybp) may show negative EF ancestry values. In sum, of the samples that passed the plausibility criteria of p-value ≥ 0.01, Steppe ancestry [0, 0.05] and EF ancestry S.E. ≤ 0.022, only ~ 3.8% and ~ 3.3% were filtered due to negative EF and WHG ancestry estimates, respectively. Under these conditions, we followed standard qpAdm⁶² practices and excluded individuals with negative ancestry proportions from downstream analyses. This filtering step ensures that only biologically interpretable ancestry estimates are included in our regressions and simulation-based inference approach and improves model robustness across diverse European Neolithic samples.

Finally, we acknowledge that reliance on a single aDNA database (in this case, AADR v62.0)⁶¹ has the potential to introduce bias. However, the AADR⁶¹ remains one of the most comprehensive, well-curated, and widely used sources of publicly available ancient DNA data. Moreover, recent work by Schmid et al.¹⁰⁵ comparing the AADR⁶¹ and the Poseidon database—another large, community-maintained ancient DNA resource—demonstrates substantial overlap between the two, particularly for European samples. This concordance across independently maintained datasets suggests that our sample set reflects the broader landscape of available ancient genomes relevant to our study.

We visualized broad genetic ancestry patterns of the analyzed individuals through principal component analysis (PCA) (Supplementary Fig. 17) using the smartpca v.8.0 software¹⁰⁶ with parameters “numoutevec: 10”, “numoutlieriter: 0”, “hiprecision: YES”, “shrinkmode: YES” and “lsqproject: YES”, projecting the ancient individuals onto a set of 69 modern Eurasian individuals⁴⁹. A complete metadata table for each of the ancient individuals can be found in Supplementary Data File 1 and ancestry estimates for all ancient individuals are located in Supplementary Data File 2.

Fitting simulations to empirical ancestry data

To fit parameters of our simulations to the qpAdm⁶² results, we compared the empirical EF ancestry estimates to the simulated ancestry clines (i.e., the EF ancestry proportion as a function of the distance to the farming origin) under different learning and within-group mating rates. Thus, for each aDNA sample in our study, we derived an observed EF ancestry proportion using the empirical estimates from qpAdm⁶², and we derived an expected EF ancestry proportion, assuming the same distance to the farming origin, from our agent-based simulations. To this end, we set the location of the farming origin on our simulation landscape just East of Ankara, Turkey, and took the straight-line distance of each ancient sample from this point. We then used our simulation data to interpolate an expected EF ancestry proportion with the same straight-line distance as each aDNA data point. We took into account uncertainty in the estimation of the empirical ancestry proportion by assuming a normally distributed measurement error with standard deviation set to the sample-specific standard error output of qpAdm⁶². For each simulated learning rate, the observed and expected EF ancestry proportions were used to calculate a log-likelihood of each ancient sample, which was then summed up across all samples. The simulation-wide log-likelihood was then plotted against each respective learning rate. We fit a quadratic function to the log-likelihood values to derive a maximum likelihood estimate of the learning rate and a standard error as the square root of the negative inverse of the second derivative (Supplementary Fig. 5; see Supplementary Note 3 for full derivation of the statistical approach).

It has been shown that the Neolithic expansion was not uniform and featured Northern (Continental), and Southern (Mediterranean) routes^45,56,69,70. To check for heterogeneity in the estimated learning rate, we fit simulated individuals along the Southern and Northern parts of the map to ancient individuals from the same regions. We used a latitude of 45 degrees as an approximate cutoff, converting our X, Y coordinate-based simulation plane to approximate latitude, longitude values to allow for comparison with aDNA data.

We also assessed if temporal ancestry variation affected our fitting results. To this end, we binned the ancient individuals by age, corresponding to three periods of the Neolithic: Early (sample age greater than 6500 ybp), Middle (sample age greater than or equal to 5500 ybp and sample age less than or equal to 6500 ybp), and Late (sample age less than than 5500 ybp). This resulted in 288 Early individuals, 206 Middle individuals, and 124 Late individuals.

To assess the robustness of our ancestry estimates to the choice of source population, we repeated the qpAdm⁶² analysis using Anatolian early farmers (n = 26) instead of Balkan early farmers (n = 21) as the proxy for Neolithic ancestry. We found that the resulting ancestry proportions produced similar spatial clines and learning rate estimates (see Supplementary Fig. 18). This suggests that our inferences are not sensitive to the specific choice of early farmer reference group, and supports the robustness of the qpAdm⁶²-based ancestry estimates. Finally, note that to derive the expected EF ancestry proportion from our simulations as a function of distance, we had to bin simulated individuals into different distance bins to compute their average ancestry proportion as a function of distance. For the simple square landscape, we binned all individuals into 20 equal-sized bins along the X-axis, since farming progresses along the X-axis from left to right in this model. On the simulated European map, where farming starts in Anatolia and then expands into Europe, we created bins based on the straight-line distance of each individual from the origin in the southeast corner of the map, representing the farming origin. We then sampled 10,000 individuals randomly throughout the map and binned them according to this distance into 100 bins with 52.4 km width, and for each bin we computed the average EF ancestry.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.